Salah satu metode maupun teknik penarikan kesimpulan dari seri penalaran deduktif dimana penalaran ini sendiri sangat sering digunakan. Bahkan Silogisme sendiri merupakan teknik yang mendasar dalam menarik suatu kesimpulan dalam matematika. Bahkan salah satu yang sering kita lewatkan adalah bagaimana teknik penarikan silogisme ini sendiri muncul. Bahkan silogisme boleh dibilang cukup sederhana daripada penarikan kesimpulan yang lain.
 |
| Silogisme dalam Matematika
© Data pribadi |
Pengertian Silogisme
Silogisme atau kaidah penelurusan sebab akibat yang menghasilkan suatu kesimpulan maupun penarikan kesimpulan yang ditelusuri dari akibat maupun sebab penyebab yang ada. Kaidah ini sendiri sangat sederhana mengingat penarikan kesimpulan semacam ini mudah untuk dipelajari. Silogisme ini sendiri terjadi apalagi terjadi pada dua pernyataan dan 1 kesimpulan.Dalam metode sederhana ini kita dituntut untuk mengerti beberapa penarikan secara silogisme. Lebih jelas adalah silogisme hipotesis. Karena saya menyederhanakannya dalam konteks logika matematika tujuannya tidak lebih ribet untuk pemula. Namun andai kata ingin mengenal lebih dalam mengenai silogisme, maka alangkah baiknya mempelajari dalam filsafat ilmu ataupun logika. Maupun saya akan menjelaskannya lain waktu.
Persyaratan khusus logika matematika Sederhana :
- Argumen ini memiliki dua premis.
- Premis pertama adalah bersyarat atau pernyataan "jika-maka", misalnya bahwa jika P maka Q.
- Premis kedua adalah bersyarat atau pernyataan "jika-maka", dengan premis kedua bagian penyebab sama dengan premis pertama bagian akibat. Contoh jika Q maka R
- Premis pertama bagian akibat (Q) harus sama dengan Premis bagian Penyebab (Q). Jikalau salah satu negatif (~Q), maka juga premis kedua juga negatif (~Q). Contoh Premis pertama P -> ~Q ; Premis kedua ~Q -> R.
- Dari kedua premis tersebut dapat disimpulan dengan menyambung premis pertama dengan premis kedua menjadi kesimpulan, Misalnya P -> Q, Q -> R, maka kesimpulan P -> R
Rumus / Aturan Silogisme Serta Pembuktian
Untuk mengerti silogisme dalam konteks logikaAturan dasar :
Tabel Kebenaran / Pembuktian Silogisme
 |
| Tabel kebenaran dari suatu silogisme (bagian B semua itu tautologi) © Data pribadi |
Bentuk lain:
Tabel Kebenaran / Pembuktian Silogisme
 |
| Tabel kebenaran dari suatu silogisme (bagian B semua itu tautologi) © Data pribadi |
Melihat kita akan menegasikan antara premis p dan r dan melihat hasil yang ada.
Aturan lanjutan 1 :
Tabel Kebenaran / Pembuktian Silogisme
Bentuk dari q negatif
Tabel Kebenaran / Pembuktian Silogisme
Aturan lanjutan 2
Tabel Kebenaran / Pembuktian Silogisme :
Bentuk dari q negatif :
Tabel Kebenaran / Pembuktian Silogisme :
Aturan lanjutan 3
Tabel Kebenaran / Pembuktian Silogisme :
Bentuk dari q negatif
Tabel Kebenaran / Pembuktian Silogisme :
Aturan dasar :
p1) Jika hari ini sedang hujan, maka saya pergi ke surabaya (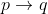 )
)
p2) Jika saya pergi ke surabaya, maka saya sedang dalam perjalanan ke kantor dengan jas hujan. (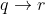 )
)
ks) Jika hari ini sedang hujan, maka saya sedang dalam perjalanan. ( )
)
p1) Jika Budi lulus ujian, maka ia tidak kuliah di Perguruan Tinggi dalam Negeri (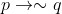 )
)
p2) Jika budi tidak kuliah di Perguruan Tinggi dalam Negeri, dirinya berkuliah di Universitas Terkenal di Luar Negeri. ( )
)
ks) Jika Budi lulus ujian, maka ia berkuliah di Universitas terkenal di Luar Negeri. ( )
)
Aturan 1 :
p1) Jika hari ini tidak hujan, maka saya keluar naik motor. (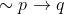 )
)
p2) Jika saya keluar naik motor, maka saya pergi ke Bandara untuk naik Pesawat ke Jakarta. ( )
)
ks) Jika hari ini tidak hujan, maka saya pergi ke Bandara untuk naik Pesawat ke Jakarta. ( )
)
p1) Jika hari ini saya tidak berpenghasilan besar, maka saya tidak dapat liburan ke Luar Negeri (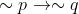 )
)
p2) Jika hari ini tidak dapat liburan ke Luar Negeri, maka saya akan mulai menabung di Bank. ( )
)
ks) Jika hari ini saya tidak berpenghasilan besar, maka saya akan mulai menabung di Bank. ( )
)
Aturan 2 :
p1) Jika hari ini saya pergi ke sekolah, maka hari ini cuaca cerah. (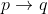 )
)
p2) Jika hari cuaca cerah, maka saya tidak membawa payung untuk berangkat ke sekolah. ( )
)
ks) Jika hari ini saya pergi ke sekoah, maka saya tidak perlu membawa payung. ( )
)
p1) Jika hari ini saya kuliah, maka saya tidak akan main-main belajar. (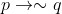 )
)
p2) Jika saya tidak main-main belajar, maka saya tidak membawa barang yang tidak diperlukan saat kuliah. ( )
)
ks) Jika hari ini saya kuliah, maka saya tidak membawa barang yang tidak diperlukan saat kuliah
Aturan 3 :
p1) Jika hari ini Budi tidak masuk kuliah, maka ia sedang sakit parah. (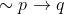 )
)
p2) Jika Budi sedang sakit parah, maka ia tidak dapat beraktivitas seperti biasa ( )
)
ks) Jika hari ini Budi tidak masuk, maka ia tidak dapat beraktivitas seperti biasa. ( )
)
p1) Jika mahasiswa tidak naik tingkat, maka ia tidak diperbolehkan mengambil mata kuliah banyak. (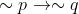 )
)
p2) Jika mahasiswa tidak diperbolehkan mengambil mata kuliah banyak, maka ia tidak akan lulus perkuliahan tepat waktu. ( )
)
ks) Jika mahasiswa tidak naik tingkat, maka ia tidak akan lulus perkuliahan tepat waktu. ( )
)
Contoh Silogisme dengan Modus Ponens
Silogisme-Ponens :
p1) Jika Budi naik motor, maka ia akan melewati rute tercepat. (p->q)
p2) Jika Budi akan melewati rute tercepat, maka ia pergi ke sekolah.
p3) Budi naik motor.
ks) Jadi Budi pergi ke sekolah.
Keterangan :
p ) Budi naik motor.
q ) Budi akan melewati rute tercepat.
r ) Budi pergi ke sekolah.
Tabel kebenaran :
Dalam progres ini, p1 dan p2 terlebih dahulu di silogismekan menjadi :
p4) Jika Budi naik motor, maka ia pergi ke sekolah.
lalu ditambah :
p3 ) Budi naik motor.
maka ketemu
ks) Jadi Budi pergi ke sekolah.
Contoh Silogisme dengan Modus Tollens :
p1) Jika Budi lulus sekolah, maka ia akan lanjut perkuliahan di perguruan tinggi.
p2) Jika Budi lanjut perkuliahan di perguruan tinggi, maka Budi akan menjadi seorang sarjana
p3) Budi tidak menjadi seorang sarjana
ks) Jadi Budi tidak lulus sekolah
Keterangan :
p ) Budi lulus sekolah
q ) Budi lanjut perkuliahan di Perguruan Tinggi.
r ) Budi akan menjadi seorang sarjana
~r ) Budi tidak menjadi seorang sarjana
~p) Budi tidak lulus sekolah
~q) Budi tidak lanjut perkuliahan di Perguruan Tinggi.
Tabel kebenaran :
Dalam progres ini sendiri p1 dan p2 terlebih dahulu menjadi
p4) Jika Budi lulus sekolah, maka ia menjadi seorang sarjana
lalu ditambah p3) Budi tidak menjadi seorang sarjana
maka kesimpulan akhir :
ks ) Budi tidak lulus sekolah.
Untuk memahami silogisme matematika logika: sebenarnya ini adalah dasar untuk melangkah pada logika dan ilmu pengetahuan lebih lanjut. Karena logika deduktif adalah awal. Namun perlu dipelajari lebih lanjut akan menghasilkan teknik penarikan kesimpulan maupun teknik penalaran yang baik. Akan lebih lanjut naik kepada logika induktif.
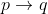
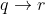
 Akan tetapi kalau di dalami akan berbeda dari apa yang ada. Dan jauh lebih jelas dari sebelumnya.
Akan tetapi kalau di dalami akan berbeda dari apa yang ada. Dan jauh lebih jelas dari sebelumnya.
Sumber :
Aturan lanjutan 1 :
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Bentuk dari q negatif
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Aturan lanjutan 2
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Bentuk dari q negatif :
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Aturan lanjutan 3
Tabel Kebenaran / Pembuktian Silogisme :
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Bentuk dari q negatif
Tabel Kebenaran / Pembuktian Silogisme :
 |
| Tabel kebenaran dari suatu silogisme
(bagian B semua itu tautologi) © Data pribadi |
Contoh-Contoh dalam Silogisme
Berikut beberapa contoh dalam prinsip sederhana silogisme dalam matematika.Aturan dasar :
p1) Jika hari ini sedang hujan, maka saya pergi ke surabaya (
p2) Jika saya pergi ke surabaya, maka saya sedang dalam perjalanan ke kantor dengan jas hujan. (
ks) Jika hari ini sedang hujan, maka saya sedang dalam perjalanan. (
p1) Jika Budi lulus ujian, maka ia tidak kuliah di Perguruan Tinggi dalam Negeri (
p2) Jika budi tidak kuliah di Perguruan Tinggi dalam Negeri, dirinya berkuliah di Universitas Terkenal di Luar Negeri. (
ks) Jika Budi lulus ujian, maka ia berkuliah di Universitas terkenal di Luar Negeri. (
Aturan 1 :
p1) Jika hari ini tidak hujan, maka saya keluar naik motor. (
p2) Jika saya keluar naik motor, maka saya pergi ke Bandara untuk naik Pesawat ke Jakarta. (
ks) Jika hari ini tidak hujan, maka saya pergi ke Bandara untuk naik Pesawat ke Jakarta. (
p1) Jika hari ini saya tidak berpenghasilan besar, maka saya tidak dapat liburan ke Luar Negeri (
p2) Jika hari ini tidak dapat liburan ke Luar Negeri, maka saya akan mulai menabung di Bank. (
ks) Jika hari ini saya tidak berpenghasilan besar, maka saya akan mulai menabung di Bank. (
Aturan 2 :
p1) Jika hari ini saya pergi ke sekolah, maka hari ini cuaca cerah. (
p2) Jika hari cuaca cerah, maka saya tidak membawa payung untuk berangkat ke sekolah. (
ks) Jika hari ini saya pergi ke sekoah, maka saya tidak perlu membawa payung. (
p1) Jika hari ini saya kuliah, maka saya tidak akan main-main belajar. (
p2) Jika saya tidak main-main belajar, maka saya tidak membawa barang yang tidak diperlukan saat kuliah. (
ks) Jika hari ini saya kuliah, maka saya tidak membawa barang yang tidak diperlukan saat kuliah
Aturan 3 :
p1) Jika hari ini Budi tidak masuk kuliah, maka ia sedang sakit parah. (
p2) Jika Budi sedang sakit parah, maka ia tidak dapat beraktivitas seperti biasa (
ks) Jika hari ini Budi tidak masuk, maka ia tidak dapat beraktivitas seperti biasa. (
p1) Jika mahasiswa tidak naik tingkat, maka ia tidak diperbolehkan mengambil mata kuliah banyak. (
p2) Jika mahasiswa tidak diperbolehkan mengambil mata kuliah banyak, maka ia tidak akan lulus perkuliahan tepat waktu. (
ks) Jika mahasiswa tidak naik tingkat, maka ia tidak akan lulus perkuliahan tepat waktu. (
Contoh Silogisme dengan Modus Ponens
Silogisme-Ponens :
p1) Jika Budi naik motor, maka ia akan melewati rute tercepat. (p->q)
p2) Jika Budi akan melewati rute tercepat, maka ia pergi ke sekolah.
p3) Budi naik motor.
ks) Jadi Budi pergi ke sekolah.
Keterangan :
p ) Budi naik motor.
q ) Budi akan melewati rute tercepat.
r ) Budi pergi ke sekolah.
Tabel kebenaran :
 |
| Tabel kebenaran dari suatu silogisme dari silogisme dilanjut ke Ponens (bagian B semua itu tautologi) © Data pribadi |
Dalam progres ini, p1 dan p2 terlebih dahulu di silogismekan menjadi :
p4) Jika Budi naik motor, maka ia pergi ke sekolah.
lalu ditambah :
p3 ) Budi naik motor.
maka ketemu
ks) Jadi Budi pergi ke sekolah.
Contoh Silogisme dengan Modus Tollens :
p1) Jika Budi lulus sekolah, maka ia akan lanjut perkuliahan di perguruan tinggi.
p2) Jika Budi lanjut perkuliahan di perguruan tinggi, maka Budi akan menjadi seorang sarjana
p3) Budi tidak menjadi seorang sarjana
ks) Jadi Budi tidak lulus sekolah
Keterangan :
p ) Budi lulus sekolah
q ) Budi lanjut perkuliahan di Perguruan Tinggi.
r ) Budi akan menjadi seorang sarjana
~r ) Budi tidak menjadi seorang sarjana
~p) Budi tidak lulus sekolah
~q) Budi tidak lanjut perkuliahan di Perguruan Tinggi.
Tabel kebenaran :
 |
| Tabel kebenaran dari suatu silogisme dari silogisme dilanjut ke Tollens (bagian B semua itu tautologi) © Data pribadi |
Dalam progres ini sendiri p1 dan p2 terlebih dahulu menjadi
p4) Jika Budi lulus sekolah, maka ia menjadi seorang sarjana
lalu ditambah p3) Budi tidak menjadi seorang sarjana
maka kesimpulan akhir :
ks ) Budi tidak lulus sekolah.
Untuk memahami silogisme matematika logika: sebenarnya ini adalah dasar untuk melangkah pada logika dan ilmu pengetahuan lebih lanjut. Karena logika deduktif adalah awal. Namun perlu dipelajari lebih lanjut akan menghasilkan teknik penarikan kesimpulan maupun teknik penalaran yang baik. Akan lebih lanjut naik kepada logika induktif.
Kesimpulan
Kesimpulan yang diambil dari penarikan silogisme adalah suatu konsep pencarian kaidah penyebab dan akibat yang didasarkan pada premis-premis sebelumnya untuk menghasilkan kesimpulan yang boleh dibilang cukup wow. Lalu kalau dilihat dari aturan maupun rumusnya sebenarnya sederhana :Sumber :
- Muhammad Rusli, I Ketut Putu Suniantara, dan Anggun Nugroho. 2018. Logika & Matematika. Yogyakarta: Andi Offset. Hlm. 15, 17
- Sukino, 2013. Matematika Untuk SMA/MA Kelas X Kelompok Wajib Semester 2, Jakarta:Erlangga, Hlm. 393
- Esti Indra Irawan dan Cucun Cunayah, 2017, 1700 Bank Soal Bimbimbang Pemantapan matematika untuk SMA/MA, Yogyakarta : Yrama Widya, Hlm.138.

Tinggalkan Komentar di bawah ini
EmoticonEmoticon