Pengertian, Notasi-Notasi, dan Penyajian Himpunan

Pernahkah kalian mencoba mengerti apakah itu Himpunan? Mungkin setiap kali kalian mengerti himpunan yang terbayang adalah sebuah tempat untuk mengelompokkan suatu jenis maupun obyek yang ada. Namun apakah kalian yang pahami dari bentuk matematika Himpunan ini?

Diagram Venn Irisan, Himpunan
© idschool.net

Himpunan sendiri banyak sekali diajarkan seiringan dengan Logika Matematika maupun dalam pembahasan diagram venn. Tetapi untuk memahami apakah itu himpunan alangkah baiknya kita mengerti dasar-dasar dari operasi himpunan ini.

Pengertian Himpunan

Himpunan dapat didefinisikan sebagai kumpulan dari objek-objek yang berbeda dengan suatu syarat yang sudah ditentukan dalam suatu kumpulan ini dan dianggap satu kesatuan. Himpunan sendiri digunakna untuk mengelompokkan sejumlah objek. Objek yang terdapat di dalam himpunan sendiri dapat didefinisikan sebagai anggota, elemen, unsur, maupun anggota. Setiap himpunan sendiri menggunakan suatu rumus yang disebut sebagai rumus himpunan. Himpunan ini sendiri mempunyai himpunan semesta (yang bersifar universal / menyeluruh) yang dinyatakan dalam notasi U maupun S.

Notasi Himpunan :

Nama --> Notasi ---> Contoh
Himpunan --> Huruf-Huruf Besar --> A, B, C, H, K, L, Q, dan lain sebagainya
Anggota --> Huruf-Huruf Kecil --> a, b, c, d, g, h, j, l, dan lain sebagainya.

Sehingga kita tidab oleh meyatakan satu himpunan itu memiliki anggota yang sama

Notasi dalam simbol-Simbol baku:
Dalam simbol-Simbol bilangan baku terdapat 6 simbol yang dapat dihafalkan menjadi :
PNZQRC :

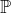 --> Himpunan bilangan Bulat Positif = {1,2,3, ...}
 --> Himpunan bilangan alami (natural) = {1, 2, ...}
 --> Himpunan bilangan bulat = { ..., -3, -2, -1, 0, 1, 2, 3, ...}
 --> Himpunan bilangan Rasional
 --> Himpunan Bilangan Rill
 --> Himpunan Bilangan Kompleks

Notasi dalam pembentuk himpunan
Aturan dalam membentuk suatu notasi pembentuk himpunan sebagai berikut :

1) Bagian di kiri tangga '{' melambangkan elemen himpunan
2) tnada '|' dibaca di mana atau sedemikian sehingga.
3) Bagian di kanan tanda '}' menunjukkan syarat keanggotaan himpunan
4) Setiap tanda ',' di dalam syarat keanggotaan di baca sebagai dan

Simbol-Simbol Himpunan :
 --> Himpuann kosong
 --> Operasi gabungan dua himpunan
 --> Operasi irisan dari dua himpunan,
 --> Subhimpunan, Subhimpunan sejati, superhimpunan, superhimpunan sejati.
 --> Komplemen
 --> Himpunan Kuasa

Penyajian Himpunan

Dalam suatu operasi himpunan kita dapa menyajikan himpunan hingga 4 penyajian. Namun secara umun selalu ada 3 penyajian. Tetapi 1 lagi ada dengan penggabungan antara simbol-simbol maupun notasi-notasi himpunan di atas.

1. Penyajian Enumerasi

Enumerasi adalah menuliskan atau mendaftarkan semua elemn himpuann yang bersangkutan diantara dua buah tanda kurung kurawal. Digunakan pada umumnya dan menuliskan suatu himpunan dengan anggota yang tidak terlalu besar. Contoh :

A = {a, b, c, d, e)
B = {1, 2, 3, 5, 8, 9, 10, }
C = {1, 2, 3 ...,  100}
D = {a, b, c, d, ..., x, y, z}
E = { ..., -3, -2, -1, 0, 1, 2, 3, ...}
F = { sapi, kambing, kerbau, kuda}
dst...

2. Penyajian dalam bentuk simbol-simbol baku. 

Dalam simbol baku-baku terdapat beberapa himpunan yang hanya menggunakan simbol-simbol diatas. Dan kerap kali digunakan secara umum agar tidak merepotkan. Misalnya simbol-simbol yang ada diatas { PNZQRC }

3. Notasi Pembentuk Bilangan

Masih dengan yang ada diatas. Kali ini menggunakan aturan notasi pembentuk suatu himpunan. Aturan tersebut ada diatas. Berikut aturan notasi pembentuk himpunan:

1) Bagian di kiri tangga '{' melambangkan elemen himpunan
2) tnada '|' dibaca di mana atau sedemikian sehingga.
3) Bagian di kanan tanda '}' menunjukkan syarat keanggotaan himpunan
4) Setiap tanda ',' di dalam syarat keanggotaan di baca sebagai dan

Contoh :
A adalah suatu himpuaan yang emiliki bilangan bulat positif yang lebih kecil dari 10. Sehingga dapat diberi bentuk himpunan berupa : A ={x|x adalah himpunan bilangan bulat positif yang lebih kecil dari 10} maupun dalam notasi bentuk lain adalah A = {x|x ∊ P, x <10} yang sama dengan A {1, 2, 3, 4, 5, ... 9}
dst ... (bisa cari di contoh internet maupun soal), karena sering ada dalam

4. Diagram Venn

Seorang matematikawan bernama John Venn sendiri memperkenalka suatu penyajian himpuann yang jauh lebih grafis maupun lebih sederhana. Sehingga memperkenalkan yang namanya John Venn. Dalam diagram Venn sendiri, himpuann semesta (U) digambarkan sebagai lingkaran di dalam segi empat tersebut.  Contoh Diagram Venn yang di dapatkan dari beberapa situs.

Contoh Diagram Venn
© www.berpendidikan.com 

Contoh Diagram Venn
© www.berpendidikan.com 

Kesimpulan 

Himpunan adalah suatu konsep matematika dimana kumpulan dari objek-objek yang berbeda dengan suatu syarat yang sudah ditentukan dalam suatu kumpulan ini dan dianggap satu kesatuan. Dalam Himpunan memiliki notasi-notasi Himpunan yang berguna untuk menyelesaikan persoalan mengenai himpunan. Himpunan sendiri dapat disajikan dalam 4 penyajian. Namun lebih sering dipakai adalah 3 penyajian, Yaitu Diagram Venn, Notasi Pembentuk Bilangan, maupun cara umum : Enumerasi.

Sumber :

https://id.wikipedia.org/wiki/Himpunan_(matematika)
Muhammad Rusli, I Ketut Putu Suniantara, dan Anggun Nugroho.  2018.   Logika & Matematika.  Yogyakarta: Andi Offset. Hlm.  29-34