Dalam hal logika, kita diharuskan untuk memberikan kesimpulan atau menarik kesimpulan akhir yang sering kali sangat menyusahkan setiap orang untuk menghasilkan suatu kesimpulan sederhana. Kadang kala gagal memberikan kesimpulan. Namun hanya berhasil menyelesaikan suatu kesimpulan yang sederhana atau hanya akan terjebak pada beberapa implikasi maupun beberapa konsep yang belum diselesaikan. Hal ini memang cukup menyusahkan mengingat kita masih awal dalam hal ini.
 |
| Penarikan Kesimpulan dalam Logika Matematika Ilustrasi © Data Pribadi |
Penarikan Kesimpulan
Menarik kesimpulan adalah suatu metode dimana kita memberikan kesimpulan dari beberapa implikasi maupun premis dan kalimat yang ada dalam matematika. Penarikan kesimpulan adalah metode sederhana untuk menghasilkan kesimpulan yang sementara dari berbagai premis yang ada.Dalam Logika Matematika sendiri lebih banyak menggunakan penalaran deduktif dimana penalaran deduktif berasal dari argumen-argumen umum ataupun argumen-argumen umum yang menghasikan suatu argumen logis yang khusus. Namun dalam penalaran ini sendiri tidak semua arumen umum itu benar dan menghasilkan argumen khusus. Sehingga kadang kala penalaran deduktif masih kurang begitu kuat ketimbang penalaran induktif. Penalaran deduktif berikut di bawah ini :
Contoh :
p1) Semua manusia pasti mati
p2) Andi adalah manusia
deduktif ) Andi pasti mati.
p1) Jika seseorang adalah kaya, pasti penghasilannya banyak
p2) Andi adalah berpenghasilan banyak
Deduktif) Andi pasti seorang yang kaya.
Dalam logika matematika kita akan mengenal 3 jenis penarikan kesimpulan, yakni Modus Ponen, Modus Tollen, maupun Silogisme. Berikut akan diungkapkan dalam sub bab Aturan inferensi yang lebih jelas isinya.
Aturan Inferensi
Aturan inferensi adalah serangkaian aturan yang dipakai untuk menginferensi / menyimpulkan suatu argumen-argumen maupun premis yang ada menjadikan suatu kesimpulan yang tepat.1. Adisi (Addition)
Adisi atau penambahan yang terjadi dalam suatu premis. Hal ini sendiri mirip dengan disjungsiAturannya :
Contoh:
p) Adam adalah belajar sangat tekun.
maka jika menggunakan adisi untuk menuliskan
q) Adam adalah pelajar di SMAN 1 Taman.
maka kesimpulannya :
2. Simplifikasi (Simplification)
Simplifikasi adalah proses untuk menyederhanakan suatu argumen maupun premis.Aturannya :
Contoh :
maka jika kita mau menyederhanakan poin diatas menjadi P, maka kita dapat menggunakan simplifikasi:
p ) Adam mahasiswa jurusan Psikologi di UNAIR.
3. Konjungsi (Conjunction)
Konjungsi adalah penghubung yang menghubungkan antara dua premis menjadi satu. Dalam aturan inferensi kita tidak menggunakan operator disjungsi, implikasi, maupun biimplikasi, akan tetapi menggunakan konjungsi.Aturannya :
Contoh :
p) Adam adalah mahasiswa yang sangat rajin mengikuti kegiatan BEM.
q) Adam adalah mahasiswa yang mendapatkan penilain terbaik di Universitasnya.
Dalam aturan konjungsi kita menggabungkan kedua premis diatas :
4. Modus Ponen (Kaidah Pengasingan)
Modus ponen sendiri sering dikaitan dengan simplifikasi karena metode yang digunakan adalah metode penghapusan atau pengasingan. Dalam kondisi logika matematika justru lebih sederhana. Namun saja ketika mencapai logika lebih lanjut kadang akan membingungkan apalagi jika sudah mendapai penalaran induktif.Aturannya :
Contoh :
p) Hari ini sedang turun hujan.
Dalam modus ponen sendiri kita dapat mengerti dalam penarikan kesimpulan yang sederhana :
q) Sudimin tidak berangkat kerja.
5. Modus Tollen (Kaidah penolakan akibat)
Modus Tollen adalah modus kedua dari ponen dimana ditinjau dari premis akibat. Dimana modus ini menyangkal isi dari penyebab. Modus Tollen adalah penyangkalan yang terjadi dalam penyebab dengan disangkal isi dari akibat:Persyaratan:
- Argumen ini memiliki dua premis.
- Premis pertama adalah bersyarat atau pernyataan "jika-maka", misalnya bahwa jika P maka Q.
- Premis kedua adalah "bukan kasus Q."
- Dari dua premis, dapat secara logis menyimpulkan bahwa "bahwa bukan kasus P.
Aturannya :
Contoh :
Dari hasil yang diperlihatkan dengan modus tollen menghasilkan :
6. Metode Silogisme (Kaidah penelusuran sebab-sebab)
Silogisme sendiri didasarkan pada penelaran deduktif dimana mencari penelusuran sebab dan akibat yang ada dalam premis-premis tersebut. Dalam metode silogisme memang metode yang sangat sederhana dan hasilnya dari pernyataan umum ke khusus. Namun untuk beberapa kasus secara KHUSUS. Silogisme maupun penalaran secara deduktif kurang ampuh. Silogisme di bawah ini adalah silogisme sederhana yang disebut dengan Silogisme Hipotesis (Hypothetical Syllogism). Berikut aturannya :Aturan 1:
Contoh :
Menggunakan metode silogisme hipotesis.
7. Silogisme Disjungsi (Disjunctive Syllogism)
Selain silogisme yang bersifat hypotensis yang sering dipakai dalam penelitian, mari kita melihat salah satu teknik lagi dari silogisme, yaitu Silogisme Disjungsi yang merupakan gabungan dari disjungsi dan silogisme. Pada dasarnya perbedaannya ada dalam premis pertama yang merupakan premis disjungsi dan mengikut kaidah tabel kebenaran disjungsi maupun implikasi.Aturannya :
Contoh :
Karena sifatnya adalah disjungsi dan silogisme adalah sebab penyebab maka kesimpulannya :
 ) Rini adalah seorang teknisi komputer.
) Rini adalah seorang teknisi komputer.
Contoh :
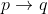 ) Jika hari ini cuaca cerah, maka saya akan pergi ke Universitas.
) Jika hari ini cuaca cerah, maka saya akan pergi ke Universitas.
 ) Jika hari ini hujan, maka saya akan tinggal di rumah.
) Jika hari ini hujan, maka saya akan tinggal di rumah.
&space;\wedge&space;(r&space;\rightarrow&space;s)) ) Jika hari ini cuaca cerah, maka saya akan pergi ke Universitas dan jika hari ini hujan, maka saya akan tinggal di rumah.
) Jika hari ini cuaca cerah, maka saya akan pergi ke Universitas dan jika hari ini hujan, maka saya akan tinggal di rumah.
 ) Hari ini cuaca cerah atau hujan.
) Hari ini cuaca cerah atau hujan.
Menggunakan metode dillema konstruktif atau jika melihat sistem silogisme konstruktif.
 ) Saya akan pergi ke Univesitas atau saya akan tinggal di rumah.
) Saya akan pergi ke Univesitas atau saya akan tinggal di rumah.
&space;\wedge&space;(r&space;\rightarrow&space;s))
Contoh :
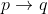 ) Jika saya lulus dengan gelar sarjana Pendidikan Matematika, maka saya akan mengajar di SMA.
) Jika saya lulus dengan gelar sarjana Pendidikan Matematika, maka saya akan mengajar di SMA.
 ) Jika saya lulus dengan gelar sarjana Biologi Murni, maka saya akan ingin melanjut S2 Jurusan Biologi untuk menjadi dosen.
) Jika saya lulus dengan gelar sarjana Biologi Murni, maka saya akan ingin melanjut S2 Jurusan Biologi untuk menjadi dosen.
&space;\wedge&space;(r&space;\rightarrow&space;s)) ) Jika nanti saya lulus dengan gelar sarjana Pendidikan Matematika, maka saya akan mengajar di SMA dan jika nanti saya lulus dengan gelar sarjana Biologi Murni, maka saya akan ingin melanjut S2 Jurusan Biologi untuk menjadi dosen.
) Jika nanti saya lulus dengan gelar sarjana Pendidikan Matematika, maka saya akan mengajar di SMA dan jika nanti saya lulus dengan gelar sarjana Biologi Murni, maka saya akan ingin melanjut S2 Jurusan Biologi untuk menjadi dosen.
 ) Saya tidak lulus dengan gelar sarjana Pendidikan Matematika atau saya tidak lulus dengan gelar sarjana Biologi
) Saya tidak lulus dengan gelar sarjana Pendidikan Matematika atau saya tidak lulus dengan gelar sarjana Biologi
CATATAN : Sering-Seringlah berlatih soal-soal logika agar dalam menarik suatu kesimpulan bisa tepat sasaran. Meskipun dalam modus ponen, tollens, maupun silogisme pasti akan susah untuk mencapai kesimpulan yang tepat. Untuk melatih berbagai logika ini alangkah baiknya membeli buku psikotes, test-test logika, psikologi, maupun matematika logika. Lebih lanjut dalam perkuliahan mungkin akan dipelajari dalam matematika distrik.
Diatas merupakan teknik-teknik yang sederhana dan dasar dari suatu penarikan kesimpulan. Meskipun dijabarkan sendiri hampir 9 jenis. Namun pada hakekatnya merupakan gabungan dan penalaran lebih lanjut. Untuk mempelajari ini alangkah baiknya mencari soal-soal maupun sering berlatih atau memasuki perkuliahan matematika distrik atau untuk melatih logika memasuki mata kuliah logika.
Sumber :
8. Dilema konstruktif
Salah satu materi susah ketika kita menemukan suatu dilema yang ada. Dilema terjadi ketika modus ponen sendiri digabungkan dengan modus ponen lainnya menghasilkan dua modus ponen yang ada dalam suatu dilema. Atau bisa dikatakan dua modus ponen yang dijadikan satu dengan penyambung dari konjungsi. Dalam Dilema konstruktif kita bisa saja sebut dengan Siloisme Kontruktif jika teknik penyampaiannya secara silogisme. Kita dapat mempelajari dari aturan di bawah ini:Contoh :
Menggunakan metode dillema konstruktif atau jika melihat sistem silogisme konstruktif.
9. Dilema Destruktif (Destructive Dilemma)
Dilema Destruktif adalah dua gabungan dari dua gabungan argumen yang dibentuk dari dua modus Tollen yang menjadi satu dalam suatu dilema tersendiri. Sehingga membentuk suatu dilema yang membingungkan kadang sudah masuk akal. Namun pada prinsipnya cukup sederhana jika menggunakan penalaran deduktif, meskipun ini sudah merupakan tingkatan lebih lanjut. Namun kita dapat mempelajarinya dalam penarikan kesimpulan. Dalam hal tertentu kita dapat menggunakan metode silogisme destruktif dalam hal dilema destruktif. Aturannya :Contoh :
maka dengan menggunakan dilema destruktif maupun metode silogisme destruktif akan menghasilkan kesimpulan :
(angan-anga bisa jadi si "saya" lulusan teknik)
CATATAN : Sering-Seringlah berlatih soal-soal logika agar dalam menarik suatu kesimpulan bisa tepat sasaran. Meskipun dalam modus ponen, tollens, maupun silogisme pasti akan susah untuk mencapai kesimpulan yang tepat. Untuk melatih berbagai logika ini alangkah baiknya membeli buku psikotes, test-test logika, psikologi, maupun matematika logika. Lebih lanjut dalam perkuliahan mungkin akan dipelajari dalam matematika distrik.
Kesimpulan
Dalam menarik suatu kesimpulan sebenarnya dari suatu teknik yang sangat mudah. Terlebih dasar untuk menarik kesimpulan menggunakan penalaran lebih sederhana, yakni penalaran deduktif. Dalam menarik kesimpulan sebenarnya ada 3 bagian yang sangat penting, yaitu modus ponen, modus tollen, maupun silogisme.Diatas merupakan teknik-teknik yang sederhana dan dasar dari suatu penarikan kesimpulan. Meskipun dijabarkan sendiri hampir 9 jenis. Namun pada hakekatnya merupakan gabungan dan penalaran lebih lanjut. Untuk mempelajari ini alangkah baiknya mencari soal-soal maupun sering berlatih atau memasuki perkuliahan matematika distrik atau untuk melatih logika memasuki mata kuliah logika.
Sumber :
- https://id.wikipedia.org/wiki/Modus_tollens
- Muhammad Rusli, I Ketut Putu Suniantara, dan Anggun Nugroho. 2018. Logika & Matematika. Yogyakarta: Andi Offset. Hlm. 13 - 18
- Sukino, 2013. Matematika Untuk SMA/MA Kelas X Kelompok Wajib Semester 2, Jakarta:Erlangga, Hlm. 392 - 394
- Esti Indra Irawan dan Cucun Cunayah, 2017, 1700 Bank Soal Bimbimbang Pemantapan matematika untuk SMA/MA, Yogyakarta : Yrama Widya, Hlm.136 - 138

Tinggalkan Komentar di bawah ini
EmoticonEmoticon